4419. Dense forest

 

To prevent the appearance of sanitary inspection in the camp, the LKSH administration dug the only road connecting the “Berendevy polyany” with Sudislavl, so now it is impossible to travel along it. However, the difficulties did not stop the inspection, for it remains only one possibility – to reach the camp on foot. As you know, Sudislavl is in the field, and “Berendevy polyany” are in the forest.

·        Sudislavl is located at the point with coordinates (0, 1).

·        “Berendevy polyany” are located at the point with coordinates (1, 0).

·        The border between the field and forest is a horizontal line y = a, where a is some number (0 ≤ a ≤ 1).

·        The speed of sanitary inspection through the field is Vp, the speed through the forest is Vf. Along the border it is allowed to move either by forest or by field.

The LKSH administration want to know how much time left to prepare for sanitary inspection visit. It asked you to find out at what point the sanitary inspection should enter into the forest to reach “Berendevy polyany” as fast as possible.

 

Input. First line contains two positive integers Vp and Vf (1 ≤ Vp, Vf ≤ 105). Second line contains one real number – the Oy coordinate of the border between the forest and field a (0 ≤ a ≤ 1).

 

Output. Print one real number with accuracy of no less than 8 digits after the decimal point – the Ox coordinate of the point at which the sanitary inspection will enter the forest.

 

Sample input

Sample output

5 3

0.4

0.783310604

 

 

SOLUTION

ternary search

 

Algorithm analysis

Let the point A of intersection of the border field / forest have coordinates (x, a). The distance from Sudislavl to point A equals to gp(x) = . The distance from point A to Berendeyev Polyany is gf(x) = . The travel time from Sudislavl to Berendeyev Polyany is

g(x) =  +  =  +

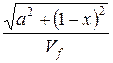
It remains to find the minimum of the function g(x) on the interval x Î [0; 1]. This can be done with ternary search.

 

Algorithm realization

Determine the distance from Sudislavl to Berendeyev Polyany as a function t depending on the abscissa x of the border between the forest and the field.

 

double t(double x)

{

  return sqrt(x*x + (1 - a)*(1 - a)) / vp +

         sqrt(a*a + (1 - x)*(1 - x)) / vf;

}

 

The main part of the program. Read the input data.

 

scanf("%lf %lf %lf",&vp,&vf,&a);

 

Run ternary search to find the minimum of the function t(x) on the segment [0; 1].

 

Left = 0; Right = 1;

while(Right - Left >= EPS)

{

  f = Left + (Right - Left) / 3;

  g = Right - (Right - Left) / 3;

  if (t(f) < t(g)) Right = g; else Left = f;

}

 

Print the answer – the abscissa of the point where the sanitary inspection should enter the forest.

 

printf("%.9lf\n",Left);